Fractal Dimensions – 
Twilight Zone?  No, Nature!

 Familiar with one, two, and three dimensions?  What about dimensions of 0.63 or 1.26?  It’s not science fiction, but quite natural.  Read on...

A group of scientists is calculating how fast a chicken can fly.  The physicist begins – “Let us first assume a spherical chicken …”

This is a favorite punch line of physics jokes.

What brings a smile to the face is that the joke makes a point about the absurdity of some assumptions.  The real world is not nice and smooth and symmetrical, like straight lines, circles, squares, spheres, cubes, and such.  If it were, it would greatly simplify calculations.

The French mathematician Benoît Mandelbrot was one of the first to bring fractal geometry to our consciousness, which can be used to describe nature more accurately.  He coined the term, “fractal,” derived from the Latin fractus meaning “broken” or “fractured.”

A fractal can be defined as having the following features:

It is too irregular to be easily described in traditional Euclidean geometry.

It is self-similar (at least approximately).

It has a fine structure at arbitrarily small scales.

It can have a dimension which is greater than its topological dimension.

It has a simple and recursive definition.

Natural objects that approximate fractals include clouds, mountain ranges, lightning bolts, coastlines, snow flakes, tree leaves, the convoluted surfaces of our brains, even some of the vegetables we eat.

Cauliflower, for example, has a feature of self similarity.  The whole cauliflower has a defining shape.  Yet, if you break off a branch, you see the same type of shape as the whole cauliflower.  Likewise, one of the flowers on the branch has the same type of shape as well.  And so on …

 
Ferns are fractal in nature and can be modeled on a computer by using a recursive algorithm.  For example, a frond from a fern is a miniature replica of the whole.

 
One of the features of fractal geometry is its fractal dimension – the measure of a set of points that characterizes its space-filling properties.  To get a handle on fractal dimensions, familiar Euclidean objects will be discussed, and then some examples of fractals.

Take an object (line, square, or cube) residing in a space of dimension, D.  Reduce its linear size by 1/l in each spatial direction.  As l increases, the number, N, of objects (lines, squares, or cubes) to fill the space increases as N = l ^D.

 
Picture and public domain info from Wikimedia Commons:  http://en.wikipedia.org/wiki/Image:Fractaldimensionexample.PNG
 

   …
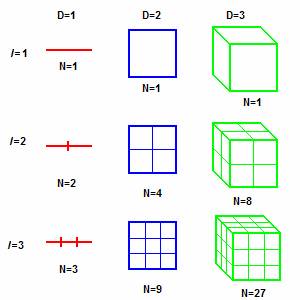
l = n       N =n¹            N = n²             N = n³

Fractal dimensions:

There are many definitions of a fractal dimension and none of them should be treated as the universal one.  I will concentrate on the capacity dimension, D_cap.

Consider  D = log(N)/log(l).

For D, take the limit as 1/l → 0 to reduce its linear size in each direction to be infinitesimally small (hence, take the limit as l → ∞):

D_cap  = lim _{l →∞} log(N)/log(l).

With this definition, the capacity dimension, D_cap, need not be an integer.  It can be a fraction or an irrational number, as we shall see.

First, D_cap will be applied to familiar 1, 2, and 3 dimensional objects – lines, squares, cubes – then to fractals.

 One dimension:

Consider a line of finite length.  Reference previous figure for D = 1.

l = n.  The first length is reduced by 1/2.  Next length is reduced by 1/3.  … The n^th length is reduced by 1/n.
N = n, number of lines that fill the space.

D_cap  = lim _{l →∞} log(N)/log(l).
D_cap = lim _n→∞ log(n)/log(n) 
D_cap = 1

So, the capacity dimension of a line is one.  No surprise, here.

Two dimensions:

Consider a square of finite area.  Reference previous figure for D = 2.

l = n.  The first square is reduced by ½ in each direction.  The next square is reduced by 1/3 in each direction.  … The n^th square is reduced by 1/n in each direction.
N = n², the number of squares that fill the space.

D_cap  = lim _{l →∞} log(N)/log(l).
D_cap  = lim _n→∞ log(n²)/log(n) = lim _n→∞ 2 log(n)/log(n)
D_cap = 2

So, the capacity dimension of a square is two.  Again, no surprise.

Three dimensions:

Consider a cube of finite volume.  Reference previous figure for D = 3.

l = n.  The first cube is reduced by ½ in each direction.  Next cube is reduced by 1/3 in each direction. … The n^th cube is reduced by 1/n in each direction.
N = n³, number of cubes that fill the space.

D_cap  = lim _{l →∞} log(N)/log(l).
D_cap = lim _n→∞ log(n³)/log(n) = lim _n→∞ 3 log(n)/log(n)
D_cap = 3

So, the capacity dimension of a cube is three.  The trend is obvious.

Fractal dimensions:

Capacity dimension becomes more interesting and complex when dealing with fractals.

Cantor set example:

To create a Cantor set, start with a line.  Next iteration, remove the middle third of the line.  In the resulting 2 lines, remove the middle third of each line.  In the resulting 4 lines, remove the middle third of each line. ...  In the resulting 2ⁿ lines, remove the middle third of each line.

Picture and public domain info from Wikimedia Commons:  http://en.wikipedia.org/wiki/Image:Cantor_set_in_seven_iterations.svg

l = 3ⁿ.  First line is reduced by 1/3 its original length.  Next line is reduced by 1/9 its original length.  … The n^th line is reduced by 1/3ⁿ  its original length.
N = 2ⁿ , number lines to fill the set:  1 line, 2 lines, 4 lines, …,  2ⁿ lines.

D_cap  = lim _{l →∞} log(N)/log(l).
D_cap  = lim _n→∞ log(2ⁿ)/log(3ⁿ) = lim _n→∞ ( n log(2) ) / (n log(3) ) = log(2) / log(3)
D_cap = 0.6309 …

In the Cantor set as l → ∞, we have an object with a dimensionality less than one, approximately, 0.6309.

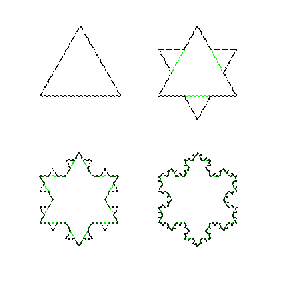
Koch snowflake example:

Another example of a fractal is a Koch snowflake.  Start with an equilateral triangle.  Next iteration, remove the middle third of each line in the triangle, and replace it with two lines, in which each has the same length (1/3) as the remaining lines.  For the following iterations, for each line, repeat the previous process.  For each successive iteration, the number of lines on each side of the Koch snowflake increases by a factor of 4.

Picture and license agreement for use from Wikimedia Commons:  http://en.wikipedia.org/wiki/Image:KochFlake.svg

l = 3ⁿ.  First line is reduced by 1/3 its original length.  Next line is reduced by 1/9 its original length. … The n^th line is reduced by 1/3ⁿ  its original length.
N = 3 · 4ⁿ , the number of lines that comprise the perimeter of the snowflake, which is three multiplied by a factor of 4 for each successive iteration.

D_cap   = lim _{l →∞} log(N)/log(l).
D_cap   = lim _n→∞ log(3 · 4ⁿ)/log(3ⁿ)
D_cap  = lim _n→∞ ( log(3) + n log(4) ) / n log(3)
D_cap  = lim _n→∞ ( log(3))/n log(3) ) + lim _n→∞ ( n log(4) ) / (n log(3) ) 
D_cap  =  log (4) / log (3) = 1.2618…

For the Koch snowflake as l → ∞, we have an object with dimensionality greater than one but less than two, approximately 1.2618.

 
To see a dynamic creation of a Koch snowflake, check out:

http://upload.wikimedia.org/wikipedia/commons/thumb/f/fd/Von_Koch_curve.gif/250px-

Some applications of fractals:
 

For the Koch Snowflake as n→∞ its perimeter becomes infinite, though the perimeter clearly encompasses a finite area.

Coastline example:

The model of the perimeter of a Koch snowflake can be applied to coastlines.

Mandelbrot began his treatise on fractal geometry by considering the question: “How long is the coast of Britain?”

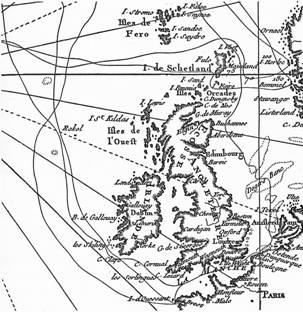
Picture and public domain info from Wikimedia Commons: http://commons.wikimedia.org/wiki/Image:Rockall_Kerguelen_map_1771.jpg

The coastline, as we see, is irregular, whether we have the view from a satellite or the microscopic view of its shoreline.  If we measure the coastline with a straight ruler, we get an estimate, which is the length of the ruler multiplied by the number of such rulers needed to cover the perimeter.  As the size of the rulers shrink, the length of perimeter gets infinitely large, much like the perimeter of a Koch snowflake.  The length of the coastline of Britain could be considered to have a fractal dimension somewhere between 1 and 2.

Wadded up paper example:

Who hasn’t taken a piece of paper, crumpled it up, and tossed it in the waste basket?  This is another example of an object which approximates a fractal.  The paper can be considered two dimensional.  Wadded up, it appears to be a spheroid shape, with irregular gaps.  Is the wad of paper 2 dimensions or 3?  Fractal geometry suggests its fractal dimension is somewhere between 2 and 3.

Conclusions:

I’ve just barely broached the subject of fractals, fractal geometry, and fractal dimensions.  Fractals are a useful model of the natural world, which can be applied in many branches of science and can be a powerful approach to analyze the complex systems around us.

 © November 7, 2008, S. K. Smith

"Canst thou lift up thy voice to the clouds, 
        that abundance of waters may cover thee?
  Canst thou send lightnings, 
        that they may go and say unto thee, Here we are?"
             Job 38: 34, 35   (KJV)